Poincare Sanısı, matematik ve fizik dünyasında büyük bir iz bırakmış olan Henri Poincaré tarafından ortaya atılmış önemli bir kavramdır. Bu makalede, Poincaré Sanısı’nın ne olduğunu, nasıl ortaya çıktığını ve günümüzdeki etkilerini inceleyeceğiz. Ayrıca, bu sanının matematiksel ve fiziksel dünyada nasıl bir rol oynadığını anlamaya çalışacağız.

Poincaré Sanısı Nedir?

Poincaré Sanısı, dinamik sistemlerin davranışlarını inceleyen bir alan olan kaotik dinamiklerde önemli bir konsepttir. Bu sanı, bir dinamik sistemin gelecekteki durumunu tam olarak tahmin etmenin olanaksız olduğunu iddia eder. Sistem, başlangıç koşullarına hassas bir şekilde bağlı olduğundan, küçük bir başlangıç değişikliği bile belirli bir noktadaki davranışı büyük ölçüde etkileyebilir.

Poincaré’nin Katkıları

Poincaré, diferansiyel denklemlerin çözümlerinin davranışını anlamak ve gelecekteki durumları tahmin etmek için geliştirdiği geometrik metotlarla ünlüdür. Belirli bir matematiksel yapının, bir ‘Poincaré bölgesi’ içindeki noktaların davranışını temsil etmek için kullanılması, sanının temelini atmıştır.

Kaotik Sistemlerdeki Önemi

Poincaré Sanısı, kaotik sistemlerin karmaşıklığını anlamak ve modellerini geliştirmek için kritik bir rol oynamaktadır. Özellikle, hava durumu, ekonomi ve biyolojik sistemler gibi karmaşık dinamik sistemlerin modellenmesinde kullanılan matematiksel araçların geliştirilmesine ilham vermiştir. Bu sistemler, Poincaré Sanısı’nın ileri sürdüğü gibi, başlangıç koşullarına büyük ölçüde duyarlıdır ve bu nedenle uzun vadeli tahminler yapmak zordur.

Matematik ve Fizikteki Etkileri

Poincaré Sanısı, matematikteki kaotik dinamikler teorisinin yanı sıra fizikte de büyük etkilere sahiptir. Özellikle, güçlü manyetik alanlar altında çekirdek parçacıkların hareketini inceleyen matematiksel modellerde sıkça kullanılır. Poincaré’nin katkıları, kuantum mekaniği ve genel görelilik teorisi gibi modern fizik alanlarının temellerini atmada önemli bir rol oynamıştır.

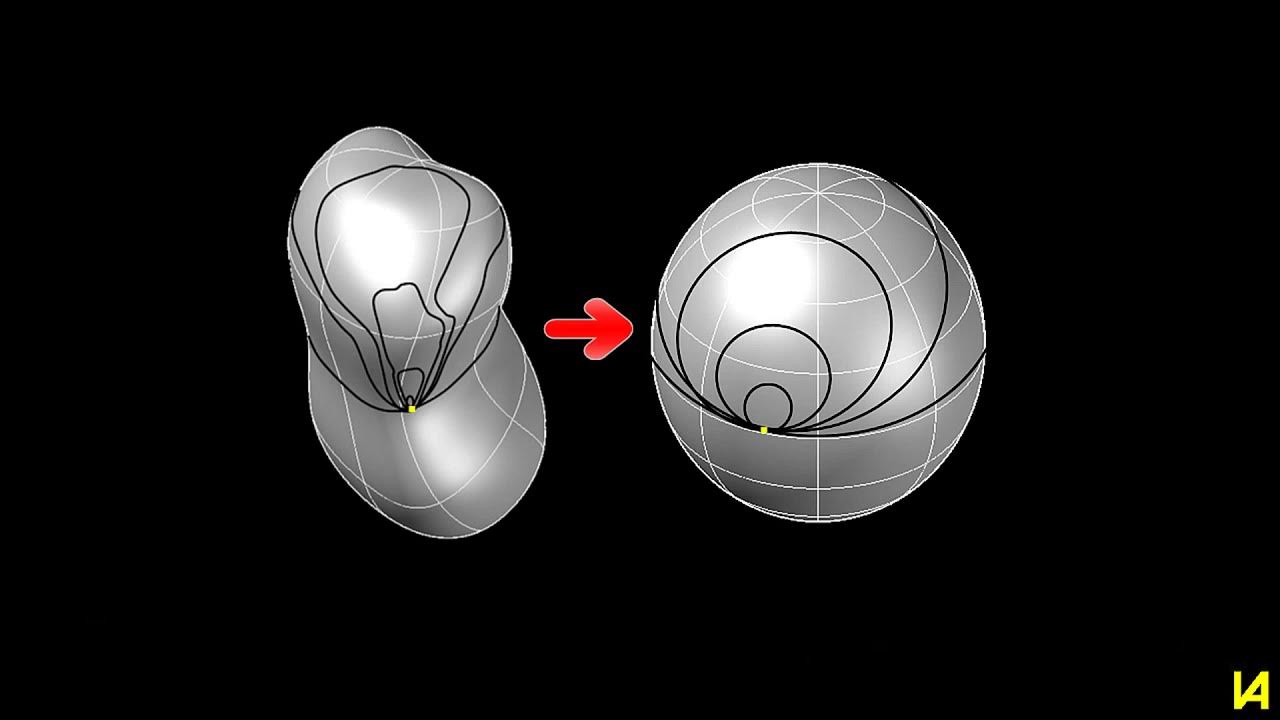
Poincaré Sanısı ve Bilinmeyenler

Poincaré Sanısı, henüz tam olarak çözülememiş bir matematiksel gizem olarak durmaktadır. Belirli dinamik sistemlerde deterministik kaosun davranışını anlamak, matematikçilere ve fizikçilere zorlu bir görev sunmaktadır. Bu, gelecekteki araştırmaların ve keşiflerin kapısını açabilir.

Sonuç

Poincaré Sanısı, kaotik sistemlerin anlaşılması ve modellenmesi konusundaki temel bir konsept olarak matematik ve fizik dünyasında hala büyük bir öneme sahiptir. Henri Poincaré’nin bu sanısı, belirsizlik ve karmaşıklık içindeki düzeni anlamaya yönelik sonsuz bir çabanın parçasıdır. Bu gizem, gelecek nesillerin matematiksel ve fiziksel evrenin sınırlarını daha iyi anlamasına katkıda bulunabilir.