Hodge Sanısı (Konjektürü) Cebirsel geometri ve topoloji, matematiğin heyecan verici ve karmaşık dalları arasında önemli bir yer tutar. Bu dallardan biri olan Hodge Konjektürü, cebirsel manifoltların topolojik özellikleri ile ilgili heyecan verici bir matematiksel iddiayı temsil eder.

Hodge Konjektürü Nedir?

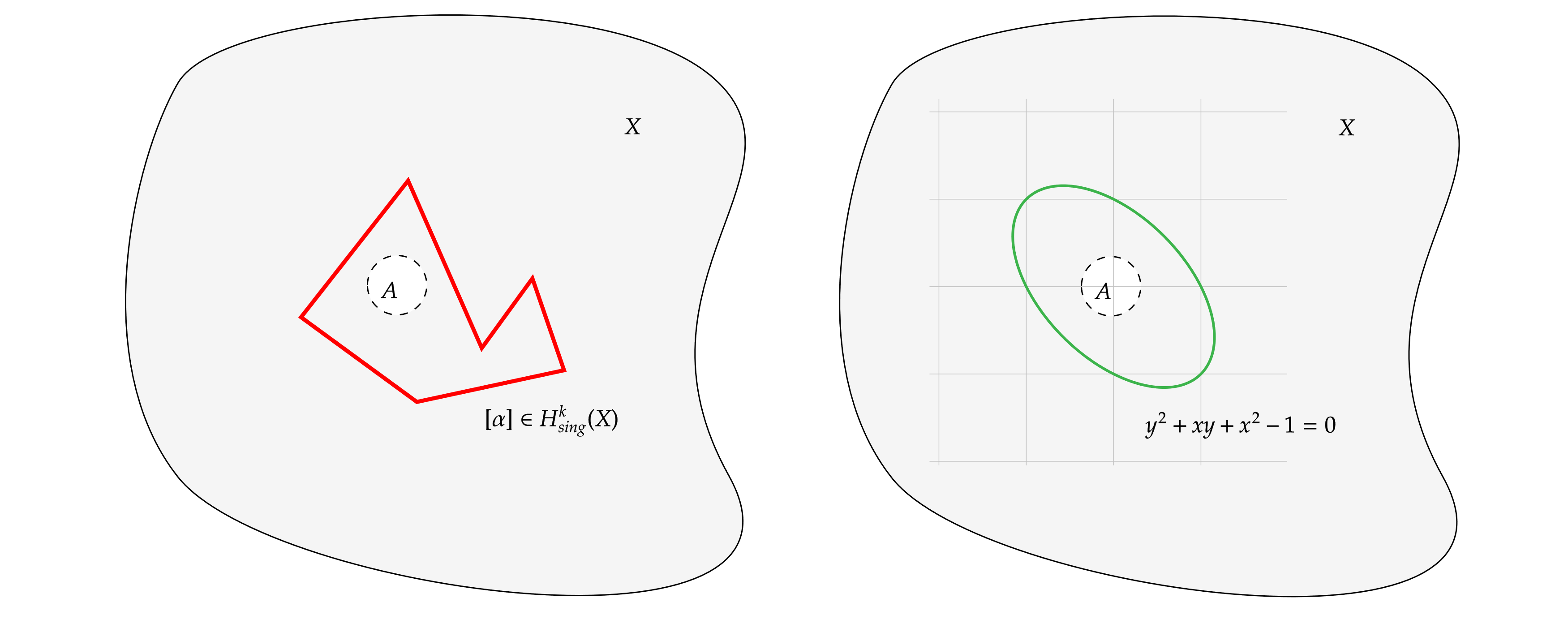
Hodge Konjektürü, cebirsel manifoltların topolojik özellikleri hakkında bir konjektürdür. Bir cebirsel manifoltun belirli bir homoloji sınıfının, manifoltun içinde temsil edilen bir Hodge yapısına sahip olması gerektiğini iddia eder. Hodge yapısı, diferansiyasyon ve integrasyon işlemlerine dayanarak elde edilen bir tür harmonik forma dayanır.

Bu konjektür, cebirsel geometri ve topoloji alanındaki önemli açıklıkları doldurmayı amaçlamaktadır. Ancak, genelde kanıtlanmamış bir konjektür olmasıyla bilinir ve matematikçiler tarafından hala çözülmeyi bekleyen bir matematiksel gizem olarak kabul edilmektedir.

Hodge Konjektürü ve Matematiksel İlerleme

Hodge Konjektürü‘nün genelde kanıtlanmamış olması, matematikteki bilimsel keşif sürecinin karmaşıklığını yansıtır. Ancak, bazı özel durumlar ve boyutlar için yapılmış kanıtlar, matematik topluluğunda bu konjektürün potansiyel doğruluğuna işaret etmektedir.

Matematikçiler, Hodge Konjektürü’nü anlamak ve kanıtlamak için yoğun çaba harcamaktadırlar. Bu konudaki ilerlemeler, cebirsel geometri, topoloji ve Hodge teorisi alanlarında yeni kapılar açabilir ve matematiğin temel yapı taşlarına daha derin bir bakış sağlayabilir.

Sonuç

Hodge Konjektürü, cebirsel geometri dünyasındaki önemli bir soru işareti olmaya devam ediyor. Matematikçiler, bu konjektürü çözmek ve anlamak için çalışmalarını sürdürerek, matematiğin gelişimine önemli katkılarda bulunabilirler. Cebirsel geometri ve topoloji severler için, Hodge Konjektürü, matematiğin içindeki bilinmeyenlerin izini sürmek için heyecan verici bir başlangıç noktasıdır.