Riemann Hipotezi, matematik dünyasının en büyük gizemlerinden biridir. Alman matematikçi Bernhard Riemann tarafından 1859 yılında ortaya atılan bu hipotez, asal sayıların dağılımıyla ilgili önemli bir iddiayı içermektedir. Bu makalede, Riemann Hipotezi’nin ne olduğunu, neden bu kadar önemli olduğunu ve üzerine yapılan çalışmaları inceleyeceğiz.

Riemann Hipotezi Nedir?

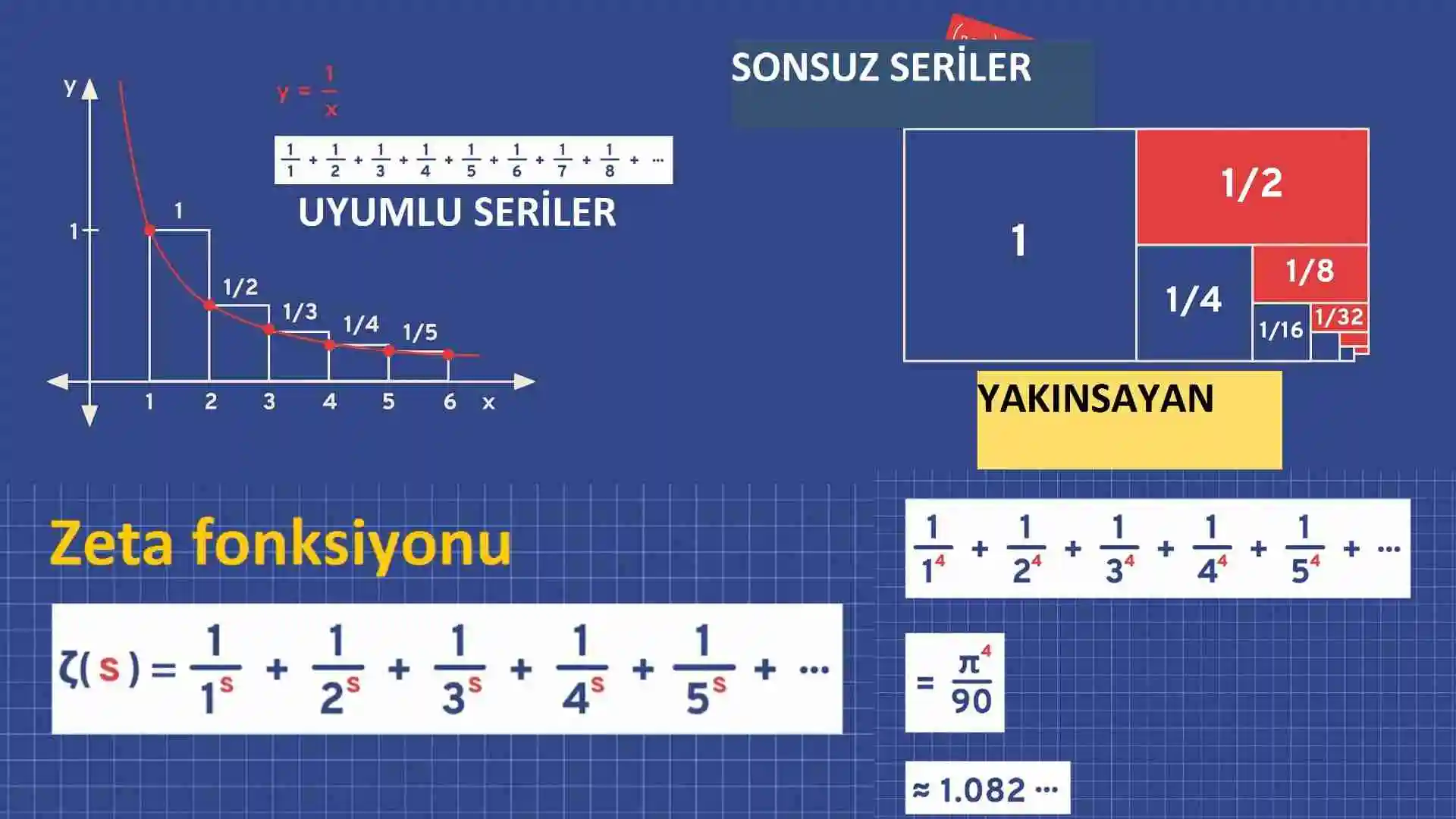
Riemann Hipotezi, Riemann zeta fonksiyonu ile ilgilidir. Riemann zeta fonksiyonu, ζ(s) şeklinde ifade edilir ve s kompleks sayılar kümesinde tanımlıdır. Hipotez, bu fonksiyonun sıfırlarının yerleşimini incelemektedir. Özellikle, Riemann, bu sıfırların tamamının belirli bir çizgi üzerinde yer aldığını iddia etmiştir. Bu çizgi, “kritik çizgi” olarak adlandırılır ve Re(s) = 1/2 ifadesiyle tanımlanır.

Neden Önemlidir?

Riemann Hipotezinin önemi, asal sayıların dağılımının daha iyi anlaşılmasına dayanmaktadır. Asal sayılar, sadece kendisi ve 1’e bölünebilen, yalnızca iki pozitif bölen içeren sayılardır. Asal sayıların nasıl dağıldığı, sayı teorisindeki temel sorulardan biridir.

Eğer Riemann Hipotezi doğruysa, asal sayıların dağılımıyla ilgili birçok sorun çözülebilir. Bu hipotezin çözülmesi, matematikteki birçok diğer problemin de çözülmesine katkı sağlayabilir.

Riemann Zeta Fonksiyonu ve Kritik Çizgi

Riemann zeta fonksiyonu, ζ(s) = 1^(-s) + 2^(-s) + 3^(-s) + … şeklinde tanımlanır. Bu fonksiyon, gerçek sayılar kümesinde belirli bir aralıkta s alındığında sonsuza yakınsar. Ancak, Riemann Hipotezi’nin odaklandığı şey, bu fonksiyonun s kompleks sayılar kümesindeki sıfırlarıdır.

Kritik çizgi, Riemann zeta fonksiyonunun sıfırlarının bulunduğu hayali ekseni bölen bir çizgidir. Eğer Riemann Hipotezi doğruysa, bu sıfırların tümü bu çizgi üzerinde yer almalıdır. Ancak, şu ana kadar bu iddia kanıtlanmış değildir ve matematikçiler bu konudaki çalışmalara devam etmektedir.

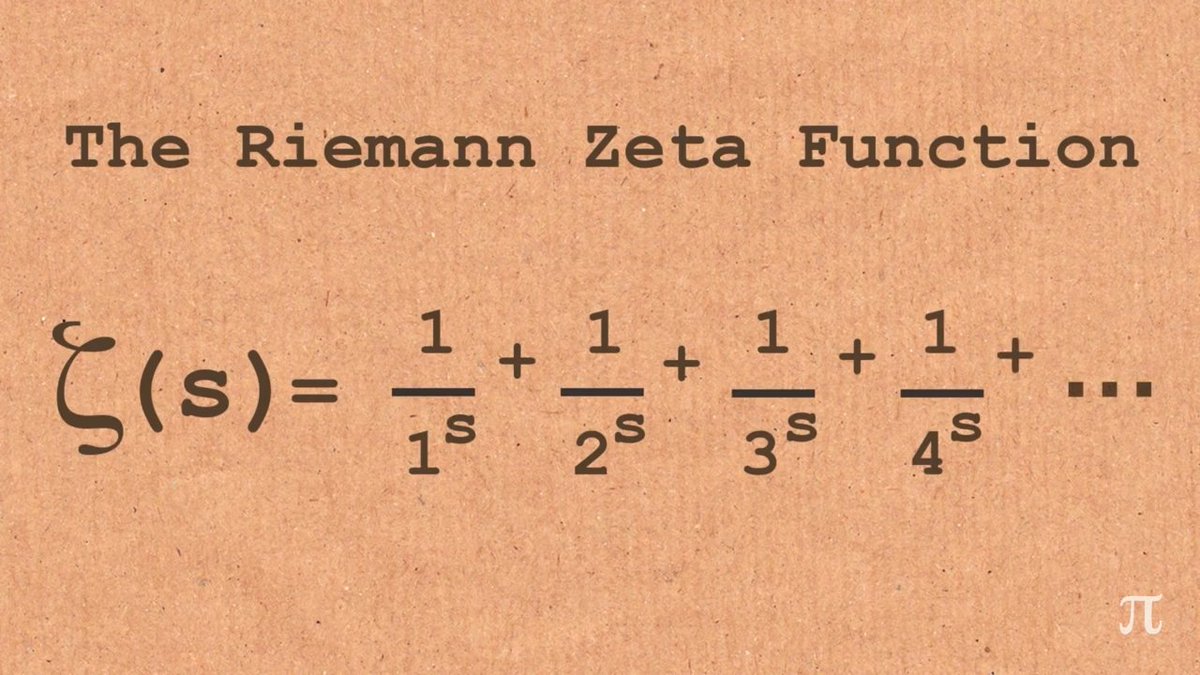
Riemann Hipotezi’nin Güncel Durumu

Riemann Hipotezi, hala çözülememiş bir matematik problemidir. Birçok matematikçi, bu hipotezi kanıtlamak veya çürütmek için çeşitli yöntemler denemiştir, ancak şu ana kadar kesin bir sonuca ulaşılamamıştır. Hipotezin doğruluğunu veya yanlışlığını kanıtlamak, matematik dünyasında büyük bir ödül olan Clay Matematik Enstitüsü’nün yedi “Milenyum Ödülü” arasında yer almaktadır.

Sonuç

Riemann Hipotezi, matematik dünyasının en karmaşık ve çözülememiş sorunlarından biridir. Asal sayıların gizemli dünyasını anlamak için büyük öneme sahip olan bu hipotez, matematikçileri yıllardır meşgul etmektedir. Belki de gelecekte, bir matematikçi bu büyük gizemi çözecek ve Riemann Hipotezi’nin doğruluğunu veya yanlışlığını kanıtlayacaktır.